Top 8 of 08: Number 6

Number 6: Sammy Wanjiru in Beijing - too hot to handle

Number 6 on our Top 8 of '08 takes us back to Beijing to look a little more closely at Sammy Wanjiru's remarkable marathon victory in Beijing.

If you needed any reminder of it, Wanjiru became Kenya's first Olympic Marathon champion (in itself an incredible fact given the Kenyan dominance over marathon running) by scorching his way to a win in 2:06:32.

It was an Olympic record, one of the fastest marathons ever run, in a race without pace-makers, and most significantly of all, in hot and humid conditions. The graph below shows the splits from the race, for those who missed it.

There are many reasons why this run was so spectacular, both as a spectator and from the scientific point of view (which is, after all, the theme of this Top 8 series).

The pacing - last man standing

Firstly, you'll notice that the pace early on was almost on world record pace. Given that the temperatures were at least 10 degrees higher than is usually the case for the elite marathon runners, combined with high humidity, this was aggressive front-running the likes of which we've never seen.

The result is seen in the overall pacing strategy of the race - only one athlete in the whole race managed to run a negative split. That was an Italian who came 15th in a 2:14 time.

Wanjiru was the best of the top 10 men - his first half was run in 62:34, his second in 63:58, a difference of 1:24. That's huge for men at this level, who normally run close to even pace, but consider that Wanjiru's rivals were blown away by almost three minutes, and you realise that the Beijing conditions were so tough that the best runners in the world lost five or six minutes in the second half of the race. Incredibly, the average difference between first and second halves for the Top 10 was 4:03, testament to the conditions and the brutality of the pace set by Wanjiru (and Martin Lel, who is one of those who faded in the second half, finishing fifth)

The heat - physiology to the fore, Las Vegas style

But that is not the reason that Wanjiru's performance scoops our sixth place of Top 8 moments.

Rather, it's because Wanjiru's win was, from a physiological point of view, proof of an observation we've made a few times here on The Science of Sport - the smaller you are, the better you'll go in the heat.

Obviously, Wanjiru is a world class athlete, perhaps the next world record holder in the marathon. His 2:06:32 in Beijing is, in my opinion, the best marathon ever run, better than what Haile G would go on to do in Berlin in October. So Wanjiru is likely to have won no matter what the conditions - hot and humid, ice-cold and windy, Wanjiru seems the class act.

But what was most interesting to me, as a scientist, is the role that Wanjiru's small size played in his victory - weighing in at only 51kg, he was one of the smallest men in the race. And size matters in the heat. You'll recall that when the body temperature rises above 40 degrees, the athlete stops running - this is the "limit" to exercise, and so if that athlete wants to finish the marathon, they must run slowly enough to prevent their temperature from hitting 41 degrees before the 42km mark.

We can calculate the increase in body temperature that would be expected if an athlete runs at a certain pace on a certain day, using mathematical models. There are theoretical predictions, of course, and should not be taken literally, but rather to illustrate a point. Take a look at the following graph, which shows the maximum possible distance that can be run at different marathon paces for two different athletes, one weighing 60kg (blue), the other 70kg (red).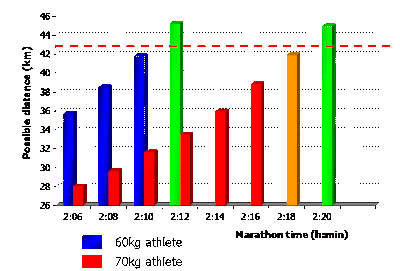


It should be immediately obvious that the smaller athlete, shown by the blue bars, is able to run further before they hit that limiting core temperature - for example, at 2:08 marathon pace, the 60kg athlete can run for just over 38 km, the 70kg athlete would make it about 30km before having to stop and cool down.

One can work out the fastest possible time that the athlete can run and still finish 42.2km. For the 60kg runner, it is about 2:10:20. For the 70kg athlete, it is 2:18:22. Again, this is not exact, because the mathematical equations don't provide exact guidelines, only illustrations of the key principle. That principle is that the larger athlete will overheat sooner on a hot day, and therefore must run slower in order to finish the race. This difference is enormous - 8 minutes thanks to 10kg of extra weight.

Now, enter Sammy Wanjiru. At 51kg, he was one of the smallest men in the race - the second smallest, if my searches were correct. Using the same formula we have above, we can work out that the theoretical limit for Sammy Wanjiru would be a 2:05:45, which means he is right on that limit, but still inside it. What he did in Beijing is therefore spectacular, impressive, but still physiologically predictable.

So predictable, in fact, that you'll find quite a nice tight correlation if you look at the order of finishers plotted against the mass of the runner. Sports science, Las Vegas style, says that if you want to place a bet on the winner, go first for the smallest runner, and then work out which small man is likely to be the best. The smaller guys tend to be better in the heat. In cooler races, this is not as significant (for other reasons, smaller athletes do tend to dominate running - this dominance is even greater in hot conditions). Just for the record, the smallest man in the race was Tsegay Kebede, of Ethiopia - he weighs in at 50kg, and he came third! Gharib, I believe, comes in at 56 kg.

So Sammy Wanjiru scoops position number 6 on our Top 8 list, thanks to his excellent demonstration of a principle of physiology. He happens to be an incredible runner too, and 2009 might just see him find his way onto the list as well, if he can get the right race on the right day, with the right pacemakers, because he's good for that world record.

Enjoy the weekend, and join us next week for the Top 5!

Ross